The Miller’s theorem establishes that in a linear circuit, if there exists a branch with impedance Z, connecting two nodes with nodal voltages V1and V2, we can replace this branch by two branches connecting the corresponding nodes to ground by impedances respectively Z / (1-K) and KZ / (K-1), where K = V2 / V1.
In fact, if we use the equivalent two-port network technique to replace the two-port represented on the right to its equivalent, it results successively:
And, according to the source absorption theorem, we get the following:
As all the linear circuit theorems, the Miller’s theorem also has a dual form:
Miller's dual theorem
If there is a branch in a circuit with impedance Z connecting a node, where two currents I1 and I2 converge, to ground, we can replace this branch by two conducting the referred currents, with impedances respectively equal to (1+ a) Z and (1+ a) Z / a, where a = I2 / I1.

In fact, replacing the two-port networkby its equivalent, as in the figure,
it results the circuit on the left in the next figure and then, applying the source absorption theorem, the circuit on the right.
Miller's theorem applies to the process of creating equivalent circuits. This general circuit
theorem is particularly useful in the high-frequency analysis of certain transistor amplifiers at
high frequencies.
The Miller Theorem (and "Effect")
Suppose that we have two networks separated by a bridging element Y. The equivalent circuits shown above represent particular important examples of such a situation
Further, suppose that we can establish the following "gain relationship" by independent means:
and, thus, we may write
If everything else remains unchanged, this bridged configuration can be replaced by a configuration of "decoupled" networks as follows:
where by equivalence we must have
The Classic Solution to the "Miller Effect"
The Cascode Amplifier
Lenny Z Perez M
EES








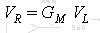





No hay comentarios:
Publicar un comentario