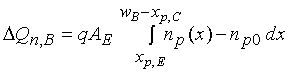The ideal transistor model is based on the ideal p-n diode model and provides a first-order calculation of the dc parameters of a bipolar junction transistor. To further simplify this model, we will assume that all quasi-neutral regions in the device are much smaller than the minority-carrier diffusion lengths in these regions, so that the "short" diode expressions apply. The use of the ideal p-n diode model implies that no recombination within the depletion regions is taken into account.
The discussion of the ideal transistor starts with a discussion of the forward active mode of operation, followed by a general description of the four different bias modes, the corresponding Ebers-Moll model and a calculation of the collector-emitter voltage when the device is biased in saturation.
Forward active mode of operation
The forward active mode is obtained by forward-biasing the base-emitter junction. In addition we eliminate the base-collector junction current by setting VBC = 0. The minority-carrier distribution in the quasi-neutral regions of the bipolar transistor, is used to analyze this situation in more detail.
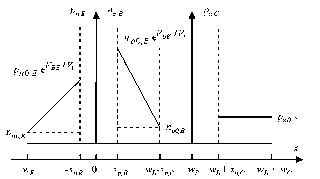
Minority-carrier distribution in the quasi-neutral regions of a bipolar transistor (a) Forward active bias mode. (b) Saturation model
The values of the minority carrier densities at the edges of the depletion regions are indicated on the Figure. The carrier densities vary linearly between the boundary values as expected when using the assumption that no significant recombination takes place in the quasi-neutral regions. The minority carrier densities on both sides of the base-collector depletion region equal the thermal equilibrium values since VBC was set to zero. While this boundary condition is mathematically equivalent to that of an ideal contact, there is an important difference. The minority carriers arriving at x = wB - xp,BC do not recombine. Instead, they drift through the base-collector depletion region and end up as majority carriers in the collector region.
The emitter current due to electrons and holes are obtained using the "short" diode expressions, yielding:
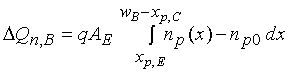
which for a "short" diode becomes:

And the emitter current due to electrons, IE,n, simplifies to:

where tr is the average time the minority carriers spend in the base layer, i.e. the transit time. The emitter current therefore equals the excess minority carrier charge present in the base region, divided by the time this charge spends in the base.
A combination of equations yields the transit time as a function of the quasi-neutral layer width, wB', and the electron diffusion constant in the base, Dn,B.

We now turn our attention to the recombination current in the quasi-neutral base and obtain it from the continuity equation

By applying it to the quasi-neutral base region and assuming steady state conditions

which in turn can be written as a function of the excess minority carrier charge, DQn,B

Next, we need to find the emitter efficiency and base transport fact

It is typically the emitter efficiency, which limits the current gain in transistors made of silicon or germanium. The long minority-carrier lifetime and the long diffusion lengths in those materials justify the exclusion of recombination in the base or the depletion layer. The resulting current gain, under such conditions, is:

From this equation, we conclude that the current gain can be larger than one if the emitter doping is much larger than the base doping. A typical current gain for a silicon bipolar transistor is 50 - 150.

This expression is only valid if the base transport factor is very close to one, since it was derived using the “short-diode” carrier distribution. This base transport factor can also be expressed in function of the diffusion length in the base:



.jpg)